Comprendre les risques extrêmes

En gestion des risques, le scénario le plus probable n’est pas nécessairement le plus important. C’est notre capacité à maîtriser les situations critiques qui est souvent déterminante. En actuariat, cette problématique est bien connue. Si le tarif, qui correspond à un scénario central dans sa version dite « pure », est un élément important, la question du niveau de réserves nécessaire pour absorber un événement de grande ampleur l’est au moins autant. La théorie des valeurs extrêmes est la branche de la statistique qui vise précisément à envisager ces issues pessimistes. Pessimistes, mais suffisamment probables pour inquiéter. Il s’agit de déterminer la hauteur potentielle de la « vague », et donc de constituer des digues financières suffisamment robustes pour lui résister.

Se préoccuper de la queue de distribution

Bien sûr, cette situation est une vue de l’esprit, car un montant de sinistre est toujours borné, même si la borne peut être extrêmement haute. Mais un tel cas de figure est le symptôme d’un modèle mathématique qui atteint ses limites, tout comme la possibilité de gérer le risque. On peut bien sûr avoir recours à différents pis-aller. Sans même parler de transfert de risque, on pourra amputer cette queue de distribution trop lourde en introduisant des limites d’indemnisation qui forcent la perte à rester contenue. On pourra même trouver hors de propos cette question de l’assurabilité. Par exemple, le cyber-risque doit bien être assurable, puisqu’il est assuré. Toute la question est bien entendu de savoir à quel point la garantie a dû être rabotée pour arriver à cette situation viable économiquement.

Car même si l’on introduit des limites d’indemnisation, on doit se préoccuper de la queue de distribution pour au moins deux raisons. D’abord parce que la lourdeur de cette queue va conditionner la valeur de cette limite. Ensuite parce que plus la situation est grave, plus une part importante du risque reste non couverte. La garantie risque de décevoir les attentes de l’assuré, lequel se rend compte qu’elle ne répond que de manière insuffisante à ses besoins. Dès lors, le risque est de dissuader de souscrire. Le volume d’affaires étant faible, le mécanisme de mutualisation opère moins efficacement, renforçant l’instabilité du résultat. Un cercle vicieux s’enclenche.

Des techniques analogues pour classifier les risques

Quels sont alors les leviers d’action ? À première vue, ils ne sont pas nombreux. Le risque s’impose à nous, on peut le réduire via, par exemple, une meilleure prévention, mais celle-ci sort du simple champ statistique. L’actuaire statisticien a pourtant un rôle important à jouer. Celui de comprendre les facteurs qui pèsent sur la queue de distribution, et d’identifier des classes de risque qui permettent une gestion différenciée.

Cet exercice fait partie de ses missions classiques. Le modèle linéaire généralisé, outil classique en tarification, est utilisé pour différencier les prix en fonction du niveau de risque. Mais cette différenciation ne s’effectue qu’au niveau du scénario central. Il faut ici développer des techniques analogues pour classifier les risques (événements, individus) en fonction de leur queue de distribution.

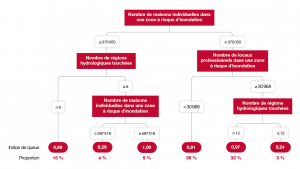
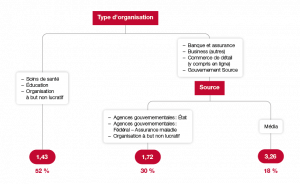
C’est le but de nos travaux récents qui mêlent outils de machine learning avec théorie des valeurs extrêmes. Dans leur version la plus simple (voir par exemple Farkas, Lopez, Thomas, 2021 (1)), nous utilisons des arbres de décision qui, malgré leur potentielle instabilité, permettent de conserver intelligibilité du modèle tout en autorisant une complexité suffisante pour capter des phénomènes non linéaires. Il s’agit, à partir des données, de constituer des classes de risques sans critères préconçus.

Segmenter pour différencier les limites d’indemnisation

Plus précisément, supposons que nous nous intéressons à un sinistre cyber. Ce terme peut recouvrir un large nombre de situations. Par exemple, concernant le type d’attaque (rançongiciel qui bloque l’accès aux données, attaque par déni de service qui sature les systèmes d’information, etc.), concernant également la victime (grande ou petite entreprise, secteur d’activité, etc.) ou encore les motivations des hackers (idéologique, chantage suivant le procédé dit de « double extorsion », etc.). Suivant le profil de l’événement, le coût ne sera bien évidemment pas le même. Classifier ces événements permet de faire le tri entre des situations particulièrement hétérogènes. En particulier, si nous nous intéressons à les classifier – non pas suivant le coût moyen de l’événement, mais en fonction de sa queue de distribution –, nous sommes capables de déterminer quelles situations peuvent être gérées facilement, et lesquelles sont susceptibles de mettre l’assureur en grande difficulté. Une fois cette segmentation effectuée, il devient possible de différencier les limites d’indemnisation suivant les types d’événements couverts et/ou les catégories d’assurés, voire de tracer une ligne entre l’assurable et le non assurable.

Il s’agit bien entendu d’un problème statistique compliqué, mais il est important de comprendre l’importance de cette classification des queues de distribution. Pour cela, revenons à l’une des idées fondamentales de la théorie des valeurs extrêmes. Selon celle-ci, les lois de probabilité se répartissent, du point de vue de leur comportement de queue, suivant trois catégories, caractérisée par une quantité appelée « l’indice de queue ». Parmi les phénomènes qu’on peut qualifier d’extrêmement volatiles, une large gamme est constituée de distributions dont la queue peut être approchée par une loi de Pareto généralisée. La méthode dite Peaks Over Threshold est l’une des techniques statistiques couramment utilisées pour effectuer une telle approximation. On s’attache à déterminer un seuil au-delà duquel l’approximation est valide, puis on ajuste les paramètres correspondants. Dit autrement, on cherche, au sein des données disponibles, les premiers signes de ce comportement de queue et on les utilise pour extrapoler la queue de distribution – sous la protection d’un résultat mathématique qui valide la méthodologie.

Que devient cette méthode dans le cas de données hétérogènes, c’est-à-dire lorsque les observations sont affectées de différents indices de queue ? Si l’on n’utilise pas l’information disponible pour cerner l’impact de caractéristiques sur cet indice, on applique la méthode Peaks Over Threshold à l’échantillon complet, laquelle est un mélange hétérogène de situations. L’analyse statistique va alors conduire à s’aligner sur le pire des cas. L’indice de queue étant une quantité non linéaire : lorsque l’on mélange des distributions, l’indice de queue qui en résulte n’est nullement une synthèse des indices des distributions qui ont été ainsi agrégées. La queue de distribution la plus lourde écrase tout le reste, même si la proportion d’événements associés à un tel cas est minoritaire.

Un grand volume de données requis

En somme, ne pas essayer de différentier entre les catégories de sinistres et/ou d’individus conduit à une analyse systématiquement pessimiste et imprécise du risque. Au contraire, parvenir à effectuer une classification plus fine fait diminuer l’incertitude et clarifie le paysage. En particulier, on sera à même de fournir des garanties plus satisfaisantes sur certains segments, sans pour autant pénaliser les catégories problématiques par rapport au traitement qu’elles auraient subis s’il n’y avait pas eu cette différentiation : contrairement à ce qui peut se passer en tarification, ne pas segmenter les populations n’équivaut pas à une forme de solidarité entre catégories. Ici, cette analyse fine ne peut faire que des gagnants, l’amélioration du résultat de chacune des parties se faisant via la réduction de l’erreur de prédiction, quand celle-ci pénalise l’ensemble des acteurs.