Risque climatique et provisionnement agricole

Le 26 novembre 2024, Marie Ganon, actuaire associée IA et consultante en recherche et développement chez Milliman, a remporté le prix Ensae Paris du meilleur mémoire d’actuariat.

Présentation

Le mémoire intitulé Prise en compte du risque climatique dans le provisionnement agricole, réalisé au sein du cabinet Milliman en 2023, s’inscrit dans une démarche de boîte à outils. Par conséquent, plusieurs approches de traitement du risque climatique pour le provisionnement ont été développées en s’appuyant sur des données d’assurance agricole.

L’une des parties du mémoire s’articule autour de l’estimation du skewness et du kurtosis de différents triangles de provisionnement (aléas climatiques, hors aléas climatiques et tempêtes, et responsabilité civile). En pratique, l’étude s’articule autour de l’application de la méthode de simulation de Dal Moro (1), qui génère les paiements de proche en proche à partir d’hypothèses sur leurs moyenne, variance et skewness jusqu’à obtention des réserves. Cette analyse vise à conjecturer une potentielle distorsion de la distribution des réserves en raison du caractère climatique du triangle.

Par ailleurs, une méthode développée par Chavez-Demoulin et al (2) a été testée afin d’affiner le calibrage de lois de sévérité pour la survenance d’événements extrêmes en tenant compte de covariables. Dans le cadre du mémoire, cette approche a été appliquée sur des pertes de rendement extrêmes, modélisées en fonction du type de culture ou encore de données d’humidité des sols. Du fait de la capacité à projeter les variables climatiques à partir de scénarios (type Giec), cette méthodologie permet d’estimer des probabilités de retour de pertes de rendement extrêmes à court terme.

Focus : Extraction d’un facteur de risque climatique à partir d’une méthode de séparation

La dernière approche développée dans le mémoire consiste en une adaptation de la méthode de séparation de Verbeek (3), initialement prévue pour capter les effets inflationnistes dans les triangles de paiements. L’adaptation proposée vise à extraire une tendance en année de survenance au sein des triangles, qui peut s’expliquer par la réalisation d’aléas climatiques, puis de la modéliser à partir de variables climatiques pertinentes. Cette dernière modélisation permet alors de mieux anticiper le provisionnement du segment étudié.

Données

Cette méthode de provisionnement nécessite de disposer d’un triangle de liquidation, supposé présentant des effets climatiques. Pour le mémoire, un triangle aléas climatiques d’assurance agricole a été exploité.

Il est également nécessaire d’avoir accès au triangle du nombre de sinistres afin d’appliquer la méthode de séparation. Pour le mémoire, du fait d’un manque de données, ce dernier a été simulé de la manière suivante.

Soient i,j les années de survenance et de développement du triangle et αM la proportion de contrats touchés par un sinistre. On suppose ensuite une proportion rj de sinistres par année de développement. À partir de ces données, on simule alors les nombres de sinistres Ni,j par une loi de Poisson de paramètre E[Ni,j]=rj×αM.

Enfin, dans l’optique de modéliser la tendance en année de survenance extraite, il faut choisir des variables climatiques pertinentes. Dans le cadre du mémoire, des données d’humidité des sols (Soil Wetness Index) disponibles sur le site de Météo France (4) ont été exploitées. Afin de projeter la tendance climatique, nous les avons complétées par des données d’humidité des sols projetées à partir des scénarios RCP du Giec et disponibles via le Climate Impact Explorer (5).

Hypothèse de séparation et adaptation

La méthode de séparation introduite par Verbeek s’appuie sur un triangle de paiements incrémentaux, noté (Xi,j) de taille I. Celle-ci repose sur une hypothèse principale sur le coût moyen des sinistres survenus en année i et déclarés en année j :

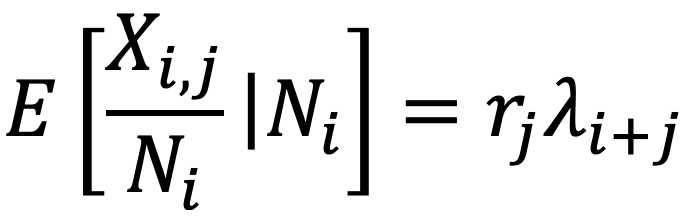
où Ni est le nombre total de sinistres survenus en année i, rj est la proportion de sinistres payés en année de développement j et λi+k est le facteur d’inflation calendaire.

À la différence de l’inflation, le climat intervient uniquement à la survenance du sinistre. En conséquence, nous ajustons l’hypothèse de séparation de la manière suivante :

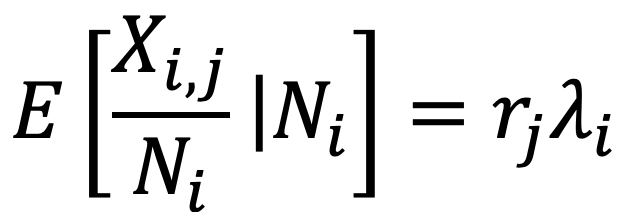C’est ce facteur λi qu’il faudra extraire pour ensuite procéder à la modélisation et la projection à partir de variables climatiques.

Estimation des réserves

Afin d’estimer les coefficients rj et λi, il est nécessaire d’avoir un bon estimateur du nombre de sinistres total Ni. Pour cela, la méthode de Mack chain-ladder est appliquée au triangle cumulé de nombre de sinistres. Après décumul, on obtient l’estimateur .

À partir du coût moyen , on peut calculer les estimateurs  et  de manière récursive :

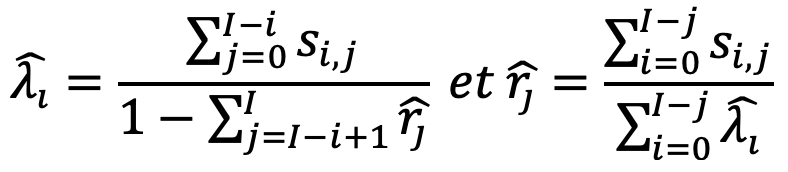
La récurrence débute en i=0 et permet d’obtenir . De là, peut être obtenu. De proche en proche, l’estimation de   est déduite de l’estimation de .

Il est désormais possible d’estimer les paiements incrémentaux futurs , puis les réserves par sommation sur les années de survenance et, enfin, par sommation totale.

Extraction, modélisation et projection de la variable climatique

Après application de la méthode de séparation climatique, nous avons pu estimer la tendance . Pour mesurer et ensuite prédire l’impact du climat sur la tendance inflationniste du triangle, il est ensuite nécessaire de modéliser cette tendance à partir des données climatiques précédemment choisies. Dans le cadre du mémoire, une régression linéaire a été effectuée à partir des données d’humidité des sols et de leurs retards. Si le modèle obtenu est significatif, alors l’application du modèle de prédiction aux données de projection conduit à la projection de la tendance climatique.

Intérêts de l’approche

Grâce à l’extraction d’un facteur d’inflation climatique au sein des triangles de provisionnement, cette méthode permet de mieux comprendre ce qui influe sur la survenance des sinistres et d’anticiper le provisionnement grâce aux projections des variables climatiques. Pour des branches telles que la sécheresse en MRH, les méthodes classiques type chain-ladder ne fonctionnent pas en raison du délai entre la survenance d’une sécheresse, la validation d’un arrêté de catastrophe naturelle et la déclaration du sinistre. Dès lors, exploiter une méthode qui projette le triangle à partir de données climatiques (températures, humidité des sols, etc.) pourrait s’avérer particulièrement intéressant afin d’anticiper l’arrivée tardive d’un certain nombre de sinistres.

Limites

Cette méthode possède toutefois quelques limites, en particulier sur la disponibilité des données.

Du côté du triangle de liquidation, il est nécessaire d’avoir des informations sur l’événement déclencheur du sinistre afin d’opter pour les variables climatiques qui auront un effet significatif sur le montant des sinistres. Par ailleurs, toujours dans cette optique, les granularités spatiale et temporelle du triangle doivent être connues.

Du côté des données climatiques, il est parfois complexe d’accéder à certains types de variables. Par exemple, pour la grêle, l’une des données les plus significatives concerne la taille des grêlons, peu renseignée dans les bases open data. Puis, il faut encore avoir accès à des projections de ces variables qui coïncident avec les données historiques. Dans le cas contraire, le triangle de liquidation ne pourra pas être complété. Enfin, pour obtenir une modélisation la plus précise possible, il est nécessaire d’aligner la granularité spatio-temporelle des variables climatiques avec celle du triangle.

Conclusion

En raison du dérèglement climatique, l’intensité et la fréquence des événements climatiques risque de s’accroître dans les années à venir. Ainsi, les assureurs devront tenir compte de ces risques dans tous les domaines de l’assurance, y compris le provisionnement. Les méthodes présentées dans le mémoire visent à anticiper l’impact des risques climatiques, que ce soit sur la forme de la distribution des réserves, les tendances observées dans les triangles ou encore les événements extrêmes.