Impact du montant de rente sur la longévité au sein d’un portefeuille de rentiers : une approche par les modèles additifs généralisés

Le risque longévité pour un assureur disposant d’un portefeuille de rentiers consiste en une sous-estimation de l’espérance de vie de ses assurés. Une espérance de vie plus élevée par rapport aux prévisions de l’assureur aboutit à des pertes financières pour ce dernier, puisqu’il doit payer des primes pour une durée plus longue que prévu, et donc en plus grande quantité par rapport à ce qui avait été provisionné au départ. La prise en compte de ce risque longévité est donc un enjeu important pour les assureurs couvrant ce type de garanties. Ceci d’autant plus que de nombreuses études tendent à montrer que l’espérance de vie humaine devrait continuer d’augmenter pendant plusieurs années encore, notamment dans les pays développés (Kontis et al. 2017). Pour tenir compte de cette espérance de vie qui évolue, des tables de mortalité prospectives sont utilisées par les assureurs pour le calcul des provisions. Leur aspect prospectif permet d’imprimer une dynamique de hausse quasi linéaire de l’espérance de vie chaque année (Debonneuil, Loisel, and Planchet 2018).

Ces améliorations de l’espérance de vie ne se font cependant pas au même rythme pour l’ensemble de la population. Il existe une certaine hétérogénéité notamment due au niveau de vie qui fait que les individus les plus aisés vivent en moyenne plus longtemps que les plus modestes (Insee, 2018). Dans le cas d’un portefeuille de rentiers, ce phénomène se traduit par le fait que les rentiers les plus riches ont une espérance de vie plus élevée que les moins riches.

L’objectif principal de l’étude menée dans ce mémoire sera ainsi de tenir compte du niveau de vie (au moyen du montant de la rente perçue) dans la construction d’une table de mortalité d’expérience prospective (calcul des probabilités de décès) pour des assurés d’un portefeuille de rentiers de l’assureur Swiss Life.

L’approche de modélisation qui sera utilisée dans ce mémoire sera celle des modèles additifs généralisés, elle ne nécessite pas une segmentation a priori de la population des assurés. Ce type de modèles est encore assez peu utilisé en Actuariat. Néanmoins, Côté (2016) présente une application intéressante de ces derniers à de la tarification en assurance automobile.

Les modèles additifs généralisés

Un modèle additif généralisé, en abrégé GAM (Generalized Additive Model), est un modèle linéaire généralisé avec des prédicteurs linéaires qui sont des fonctions lisses des variables explicatives Wood (2017).

Avec :

• μ_i≡E(Y_i)_, Y_i étant la variable d’intérêt de loi appartenant à la famille exponentielle
• g une fonction de lien
• A_iƟ correspondant à la partie paramétrique du modèle, où A_i est une ligne de la matrice de design, et Ɵ le vecteur
  de paramètre associé
• f_j une fonction lisse associée à la covariable x_j

Ce type de modèle permet une certaine flexibilité (comparativement aux modèles totalement paramétriques) dans la matérialisation des dépendances entre les différentes covariables et la variable d’intérêt.

Construction de la table de mortalité prospective

Les modèles additifs généralisés ont été calibrés sur le nombre de décès, en supposant que ce dernier suit une loi de Poisson. Nous mettrons en offset l’exposition et la force de mortalité des tables réglementaires. Pour une loi de poisson, la fonction de lien g est la fonction logarithme népérien.

Le modèle calibré s’écrit comme suit :

Avec :

• a,β1 : des coefficients qui seront estimés par le modèle
• x, d, m2, s, ec, μ : l’âge, le nombre de décès, le montant de rente, le sexe, l’exposition au risque et la force de mortalité des tables réglementaires
• S1, S2 des fonctions lisses à estimer pour l’âge et le montant de rente respectivement
• S3 la fonction lisse à estimer pour l’interaction entre l’âge et le montant de rente
• m2 la médiane de la classe de montant de rente

Effet de l’âge

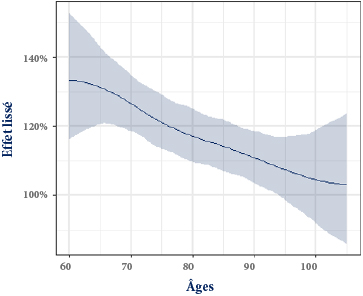
Figure 1 : Effet lisse de l’âge

Sur la Figure 1, nous observons un effet décroissant de l’âge. Ainsi, l’écart entre les décès observés dans le portefeuille et ceux prédits par les tables réglementaires tend à décroître à mesure que l’âge augmente. Une interprétation de l’effet représenté sur ce graphique est la suivante : toutes choses égales par ailleurs, pour un individu du portefeuille âgé de 60 ans, il faudrait multiplier la force de mortalité des tables réglementaires par 132 % pour obtenir la force de mortalité de cet individu dans le portefeuille.

Effet du montant de rente

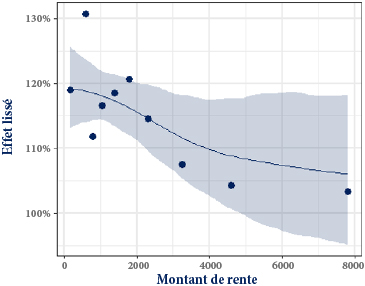
Figure 2 : Effet lisse du montant de rente

Nous constatons sur la Figure 2 une tendance à la baisse des écarts par rapport aux tables réglementaires à mesure que la médiane de la classe de montant de rente augmente. L’effet capturé ici est beaucoup plus net que ce que l’on observait avec le modèle précédent dans lequel la rente était traitée comme une variable catégorielle. De plus, le lissage élimine les fluctuations erratiques que l’on pouvait observer d’une classe de montant de rente à l’autre, ce qui semble plus proche de la réalité du phénomène étudié. L’effet capturé ici tend à se courber légèrement vers les montants de rente les plus élevés avec une pente de moins en moins raide. Ceci traduit une certaine atténuation de l’effet du montant de rente vers les montants élevés. Ceci est plutôt en accord avec la littérature sur le sujet qui stipule que les améliorations de mortalité liées au niveau de vie sont de plus en plus faibles à mesure que le niveau de vie augmente.

Effet d’interaction

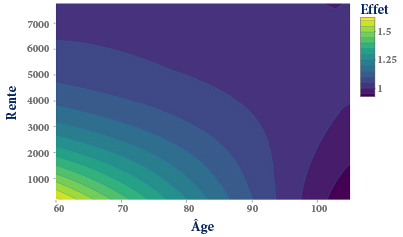
Figure 3 : Effet d’interaction entre âge et montant de rente

La Figure 3 présente les effets combinés des variables âge et montant de rente prises individuellement ainsi que l’effet de leur interaction. Il apparaît ici que plus l’âge augmente, plus un effet éventuel du montant de rente tend à disparaître (de moins en moins d’effets verticaux vers les grands âges sur le graphique), ce qui semble logique car, au-delà d’un certain âge, la mortalité est déterminée exclusivement par des facteurs biologiques liés au vieillissement.

L’effet du montant de rente a été confirmé par un modèle de Cox et par des forêts aléatoires de survie.

Calcul des provisions

Pour évaluer l’impact de la table construite, les provisions ont été calculées avec quatre modèles différents :

• Le modèle GAM ayant servi à la construction de la table
• Un modèle GAM ne prenant pas en compte le montant de rente
• Le modèle utilisé par Swiss Life
• Les tables réglementaires

Écarts globaux

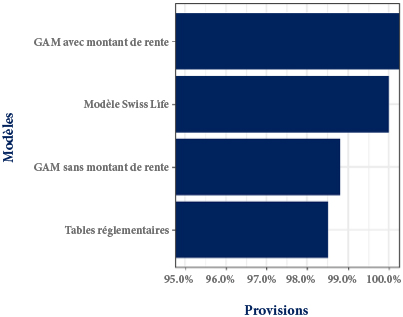
Figure 4 : Provisions globales par modèle exprimées en termes de pourcentage des provisions du modèle Swiss Life

La Figure 4 présente les provisions totales évaluées par les différents modèles en pourcentage des provisions évaluées par le modèle interne. Le premier constat ici est que les provisions évaluées suivant les deux modèles GAM et le modèle Swiss Life sont plus prudentes que les tables réglementaires. Ensuite, le modèle Swiss Life se révèle moins prudent que le modèle GAM avec montant de rente, mais plus prudent que le modèle GAM sans montant de rente.

Impact du montant de rente

Pour isoler l’effet du montant de rente, nous allons comparer les provisions du modèle GAM incluant le montant de rente et celles du modèle GAM n’incluant pas le montant de rente. Ceci permet d’éliminer les interférences qui pourraient être liées aux différences intrinsèques entre les modèles GAM et le modèle Swiss Life.

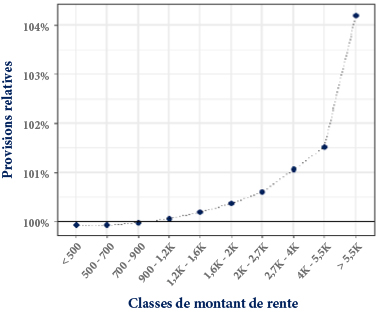
Figure 5 : Provisions par montant de rente exprimées en termes de pourcentage des provisions GAM sans prise en compte de la rente

La Figure 5 présente les provisions par montant de rente (pour le modèle GAM incluant le montant de rente) en pourcentage des provisions fournies par le modèle GAM n’incluant pas le montant de rente. On constate des écarts de provisions de plus en plus élevés à mesure que le montant de rente augmente. Ceci est assez logique vu que le modèle GAM avec montant de rente, comme vu dans le chapitre précédent, décrit une diminution de la mortalité avec le montant de rente. De ce fait, à âge et sexe inchangés, il fournit des provisions d’autant plus élevées (relativement au modèle ne prenant pas en compte le montant de rente) que le montant de rente est élevé. Nous constatons un écart maximal de plus de 4 % pour la classe de montant de rente la plus élevée.

L’objectif principal de l’étude menée dans ce mémoire était la construction pour un portefeuille de rentiers d’une table de mortalité prospective qui tienne compte du montant de rente perçu par les individus dans l’évaluation des probabilités de décès. Pour ce faire, des modèles additifs généralisés ont été utilisés. Il a été observé pour le portefeuille à l’étude une décroissance du niveau de mortalité avec l’augmentation du montant de rente. C’est un résultat cohérent au vu de la littérature sur le sujet de la longévité et de l’espérance de vie qui stipule que les individus les plus aisés vivent en moyenne plus longtemps que les individus les plus modestes.

Des provisions mathématiques ont été calculées avec la table prospective ainsi construite. Au global, les provisions obtenues via la table construite sont plus prudentes que celles obtenues avec le modèle Swiss Life ou encore les tables réglementaires. Cette étude présente un certain nombre de limites dont la principale est sans doute le fait que le montant de la rente perçue par les individus dans le portefeuille étudié ici n’est pas forcément représentatif de leur niveau de vie. En effet, il est possible par exemple que des assurés ayant des montants de rente faibles dans le portefeuille étudié ici aient d’autres contrats de rente dans d’autres compagnies, avec des rentes bien plus élevées. Il faudrait alors utiliser la somme des montants sur les différents contrats pour être parfaitement exhaustif, ce qui nous est malheureusement impossible, tandis que cette information est inaccessible.